Maths
Life but not as we know it – for Keira and Heather wondering if we might be Martians changed into humans
Hello Heather and Keira,
Firstly, let me apologise for taking two weeks to reply to your question. It has been a very busy time working on a project for a choir but I now have two weeks before the next project starts so it's time to catch up.
I now have another post for you but it may be challenging to understand some of its content. I have found the more I learn, the more I realise how little I know. Checking ideas and information for you and others when I write a post can often challenge my understanding but its by challenging ourselves to understand we can learn.
Back on the "How did Earth begin?" post I tried to answer your challenge. Like all good enquiring minds, one idea can lead to another so, in the comments section, you added...
In one of the paragraphs, we noticed that you talked about possible life on Mars. Keira thinks that over time, the sun will come too close to Earth, and Earth might shatter. That might be a possibility. There is one problem though. Martians could have died, but Mars didn’t shatter. Do you think that WE are Martians CHANGED into human?
Our minds can be a very powerful weapon against ignorance when we have curiosity and a will to find answers. This is particularly important for science as it tries to find the answers to questions. As lovers of science, your curiosity can lead you in all sorts of directions. I know mine does as I try to find answers. Let's look at a simple answer...
Do you think that WE are Martians CHANGED into human?
It's possible.
Too quick an answer?
Let's put it this way, I'm not comfortable completely ruling out many ideas. It is possible first life on Earth came from Mars but I don't think it's likely.
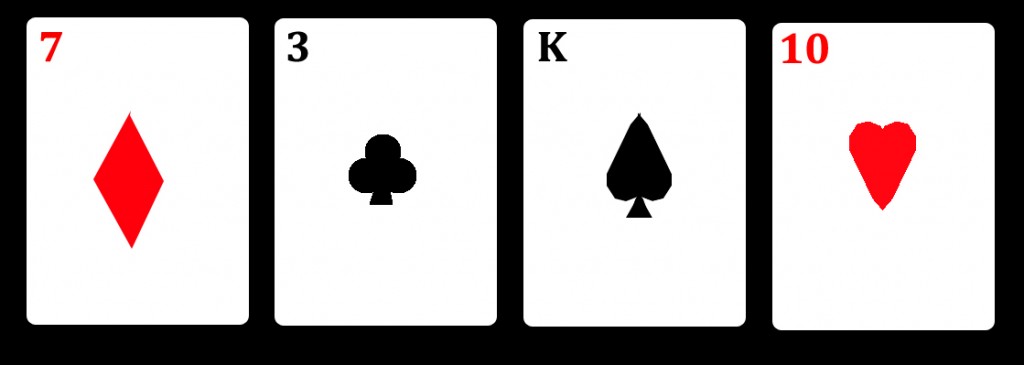
Here's some mind blowing maths for you. Just say you shuffled a deck of playing cards and put four down on the table...
When you put down the first card, the chances of it being a 7 of Diamonds is 1 in 52 because there is only one 7 of Diamonds in a deck of 52 cards. To then put down a 3 of Clubs, the chances are 1 in 51 because there were 51 cards left. For the King of Spades, it's one in 50 and, for the 10 of hearts, 1 in 49. So what is the chance of dealing just those four cards in that order from any normal deck of cards...
The chance of dealing those exact cards in that order is only 1 in 6,497,400 ... (52 x 51 x 50 x 49 = 6,497,400). It's not very likely we would get those exact four cards in that order if we shuffled and dealt four cards again but it is possible. Of course, a magician or a card trickster could cheat to get the results over and over but then the cards aren't random.
This type of maths looks at probability, i.e. chances of something happening. If we only have one card and it's the King of Clubs, the chances of dealing a King of Clubs is one in one or 100%. The chances of dealing a 7 of Diamonds is zero in one or 0% because we don't have that card. Can't maths be amazing?
For really mind blowing maths, go to the end of this post where I work out the chances of dealing out all 52 cards in an exact order, at least if I have the maths correct.
Where Did Life On Earth Come From?
I know of two main ideas for the origin of life according to science.
1. The Primordial Soup
This idea suggests billions of years ago, chemicals became concentrated (thicker) in pools of water (the primordial soup). By chance, these chemicals were able to form amino acids (the basis of life including us). In time, they combined to make more complex compounds and eventually life. This process is known as abiogenesis.
The chances of life in this way would be seen as very unlikely but, if this process is correct, it did happen. Look again at the card example in "The REALLY Mind Blowing Maths" at the end of this post. The order of cards I dealt was very unlikely but it did happen.
2. Panspermia
Some theorists suggest life might have evolved elsewhere and was brought to Earth on meteorites (Panspermia). This might be better suited to the idea life on Earth started on Mars. If life had started on Mars, a meteor strike might have thrown Mars rock into space and it may have made it to Earth but, then again, life on Earth and Mars might have come from anywhere in space. Remember, if it was life, it would have been very simple, possibly single cells, not animals like us.
No, if you watch the video clip to the end, I don't believe aliens are experimenting with us. It is possible but very unlikely. 🙂
What does Ross think?
The first idea can explain how life itself could have started, whether here or somewhere else in the universe. The second suggests how life might have made it to many places in the universe. Think of it, life might have started in many places in the universe and been spread to the stars, or at least their planets.
Did Mars Once Have Oceans and Rivers?
One of the important resources for life as we know it is liquid water. There is evidence rivers, lakes and oceans once flowed on Mars but liquid water hasn't been seen on Mars. Much of the water was probably lost to space long ago. There is plenty of evidence water as ice is found at the Martian poles and growing evidence it is to be found in the rocks and soils so life may well exist there waiting to be discovered but don't expect anything like animals running around. It's very unlikely intelligent life ever existed on Mars but is likely life did and/or does exist.
You have questioning minds so I suspect you're wondering, what happened to the Martian oceans and rivers?
Here is a video looking at the way Mars may have lost much of its atmosphere...
You may have understood the idea energy from the sun (the solar wind) caused Mars to lose most of its atmosphere so you might wonder why this didn't happen here on Earth.
Why did Earth keep its thick atmosphere while Mars lost much of its atmosphere?
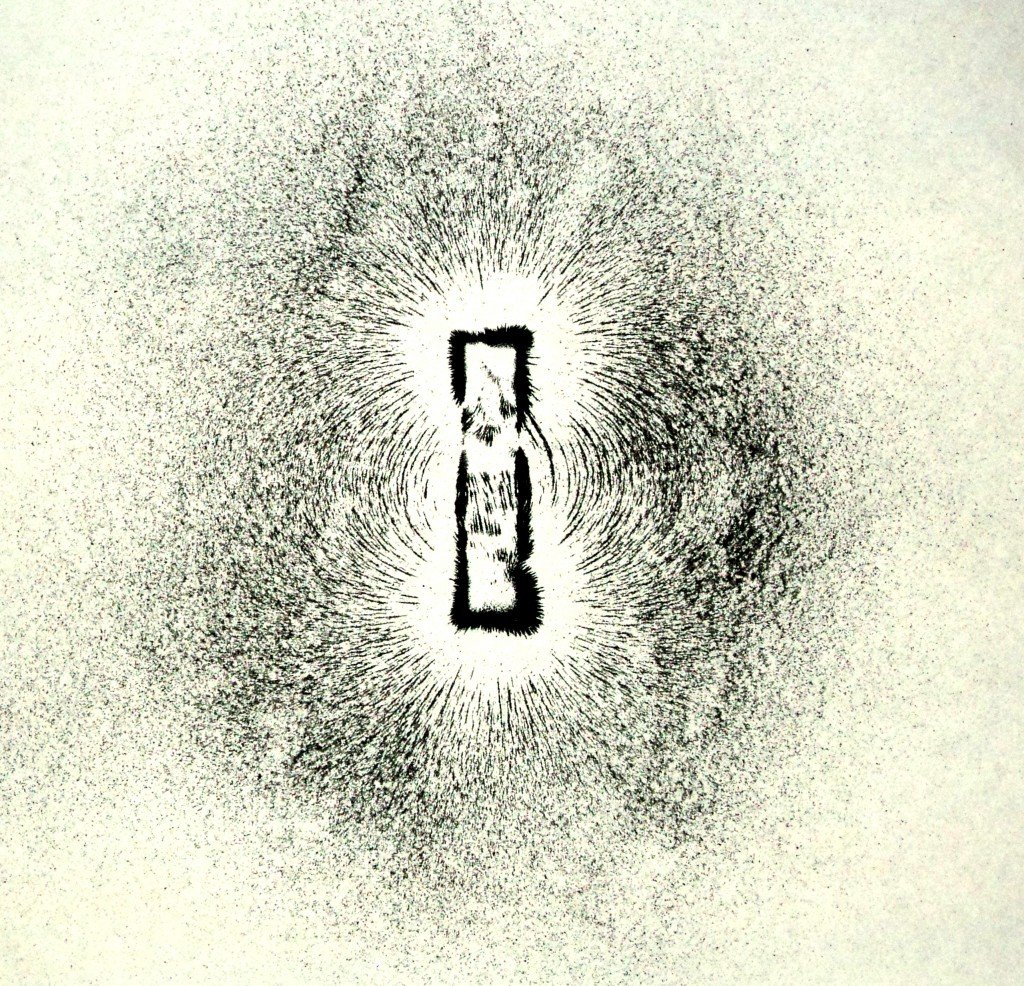
Let's first look at the photo I prepared for you. It's made by placing a magnet under a piece of paper then sprinkling iron sand over the paper.
The lines you can see in the sand help us see the magnetic field of the magnet. You can see the lines run from one end to the other of the magnet. The Earth also has a magnetic field because of its rotating iron core in its centre. The iron core helps create a much stronger magnetic field than on Mars. It protects us from much of the solar wind. Think it of a little like an umbrella in the rain.
Earth's umbrella (magnetic field) is stronger than that of Mars so we get better protection. Below is a NASA diagram showing the magnetic field of Earth. If Earth's centre cooled and slowed reducing our magnetic field or solar wind became stronger, Earth would also eventually lose much of its atmosphere.
Keira thinks that over time, the sun will come too close to Earth, and Earth might shatter. That might be a possibility. There is one problem though. Martians could have died, but Mars didn’t shatter.
Watch this video clip...
In this model of Earth's future, the Earth would eventually be pulled towards the sun and, in a sense, "shatter". Its matter would turn to plasma, a major part of the sun. I have shown Mars didn't lose much of its atmosphere because it shattered, it was lost because it didn't have a strong enough magnetic field to protect it in the way Earth is protected.
I found another video but it is harder for you to understand. It was made by a college student as an assignment looking at the life of the sun. At the stage where our sun becomes a red giant life would no longer be possible on Earth but we are looking billions of years into the future. In this model, it's not so much that the sun comes closer, it grows larger.
What will really happen in the Earth's future? Trying to find answers to what, how and why is the reason science is so interesting. We can observe, gather data, carry out experiments, discuss our ideas with others... When we have enough evidence, we can make an hypothesis (the next step up from an idea). If others find evidence supporting our hypothesis, it can take the next step and become a theory. Theories are the strongest ideas because they have much evidence to support them.
What's my idea about Earth's future? Perhaps when the sun starts threatening life on Earth, someone will press the reset button and the sun will return to a safer stage but that's even less likely than dealing the cards in the exact order below five times in a row. 🙂
The REALLY Mind Blowing Maths
Okay, the card maths at the beginning of this post seems mind blowing but it gave me an idea. If I was to deal out all 52 cards from a shuffled deck...
then shuffled the cards and asked you to deal them out in that same exact order, what would the chances be of dealing all 52 cards out one at a time in exact order without cheating or using magician tricks? Here would be the calculation...
Chance of dealing all 52 cards in an exact order = 52 x 51 x 50 x 49 x 48 x 47 x 46 x 45 x 44 x 43 x 42 x 41 x 40 x 39 x 38 x 37 x 36 x 35 x 34 x 33 x 32 x 31 x 30 x 29 x 28 x 27 x 26 x 25 x 24 x 23 x 22 x 21 x 20 x 19 x 18 x 17 x 16 x 15 x 14 x 13 x 12 x 11 x 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1
and what answer did I get?
The chances are one in ~80,658,200,000,000,000,000,000,000,000,000,000,000,000,
000,000,000,000,000,000,000,000,000.
In maths, the tilda (~) is used to mean approximately (about).
The chances of dealing all 52 cards in an exact order is so small most would think it's impossible but I had done it the first time and, by chance, you might be able to do it but it isn't very likely. 🙂
4KM and 4KJ had a maths problem to solve – I couldn’t resist sharing my solution.
To see the original post...
Today’s Problem: Sealed Solution
Hello 4KM and 4KJ,
I think you already know I love a maths challenge. Seeing your post for your special visitors, I saw the included challenge and thought I would share my solutions. For others, here was the challenge for the students and special visitors.
This problem is from the NRICH website.
There are 10 cards each bearing the digits 0 to 9. Two are placed in each of five envelopes. The sum of the two cards in each envelope must match the number on the envelope. The challenge was to find what two cards could be in the envelope numbered 8. The students and visitors were informed there was more than one solution. See the below graphic...
How did I find my solutions?
1. The challenge stated the two cards in each envelope are added to reach the number on the envelope (the sum of the two cards).
2. Being ten cards each bearing a digit from 0 to 9, I assumed each digit could only be used once.
3. Next I looked at the target, Envelope 8. Using the cards, what 2 card combinations could give the sum of 8? Here they are..
8 + 0 = 8
7 + 1 = 8
6 + 2 = 8
5 + 3 = 8
4. Now I drew up a grid to test each of the sums to see if all four could be correct. I found three worked but one failed. Here are the three successful answers...
3 + 4 = 7 8 + 0 = 8 6 + 7 = 13 9 + 5 = 14 1 + 2 = 3
2 + 5 = 7 7 + 1 = 8 9 + 4 = 13 8 + 6 = 14 3 + 0 = 3
7 + 0 = 7 5 + 3 = 8 9 + 4 = 13 8 + 6 = 14 1 + 2 = 3
Therefore, Envelope 8 could only contain 0 and 8, 1 and 7, or 3 and 5.
Why did 2 and 6 fail?
Envelope 14 can only contain 8 and 6 or 9 and 5 to give the sum of 14. As 2 and 6 (6 + 2 = 8) have been used, 8 and 6 aren't possible but what about 9 + 5 =14?
Envelope 13 can only contain 9 and 4, 8 and 5 or 7 and 6 if the sum is to be 13. If we have already used 2 and 6 (2 + 6 = 8) and 5 and 9 (5 + 9 = 14), we can't use any solution for Envelope 13. Therefore 6 + 2 = 8 is not a solution.
How did I do?
A number sequence
4KM and 4KJ have been looking at number sequences...
Number Sequences and Patterns
One student replied to a comment I wrote. The class had looked at the Fibonacci Sequence I had shared and were able to work out the next number in...
0, 1, 1, 2, 3, 5, 8, 13, 21, …
They worked out, for example, 8 came from adding the previous two numbers, i.e. 3 + 5. 13 came from adding 5 and 8. 21 came from 8 and 13. They worked out the next number would be...
13 + 21 = 34
I shared a much harder sequence of numbers I found. I think many adults might have a problem solving this one...
15, 29, 56, 108, 208, ___
Given a choice of four possible next numbers, which do you think comes next...
a) 386 (b) 400 (c) 416 (d) 438
I gave the answer as (b) 400
Why is this so?
Looking at the numbers, I first noticed each number was roughly double the previous...
15, 30, 60, 120, 240
I then looked at the difference between the doubling and the sequence number...
15, 30-1, 60-4, 120-12, 240-32
But how could we work out the pattern? The number we subtract changes. Here is the pattern...
15, 2 x 15 - 1 x 1, 4 x 15 - 2 x 2, 8 x 15 - 3 x 4, 16 x 15 - 4 x 8
Notice...
1) the number to multiply the 15 doubles each time
2) the first number in the subtracted multiplication goes up one each time
3) the second number in the subtracted multiplication doubles each time
Using these patterns, the next number in the series would use the equation...
32 x 15 - 5 x 16 = 480 - 80 = 400
If a student understands how I worked out the sequence, what number comes after 400? Leave your answer in the comments.
Is this a case of being as clear as mud? 🙂
If you know anyone keen on hard number sequences, here is a link to a few. It is a number sequence test. The above sequence is part of the test...
Number Sequence Test - Hard
Comparing Population Densities of Australia, Canada, Great Britain, New Zealand and U.S.A.
For the Mr. Avery and Class "Our World Our Numbers post"...
Our World, Our Numbers on: Population and Area
Of Australia, Canada, United Kingdom, New Zealand and U.S.A., which country is largest by population density?
Seeing a post looking at people and land area, I wondered how the population densities of Australia, Canada, United Kingdom, New Zealand and U.S.A. might compare.
Population density is how many people there are for every square kilometre or mile of land area in a country. We take the population of a country and divide by the land area.
Which country has the highest population density?
Schools and students have permission to use this graphic for non-commercial, educational purposes.
The United Kingdom
Let's look at the order of the countries according to the information I used to find the answer.
Area
1. U.S.A. (9,826,675 square kilometres)
2. Canada (9,984,670 square kilometres)
3. Australia (7,692,024 square kilometres)
4. New Zealand (268,680 square kilometres)
5. United Kingdom (243,610 square kilometres)
Population
1. U.S.A. (314,000,000)
2. United Kingdom (62,640,000)
3. Canada (34,480,000)
4. Australia (23,000,000)
5. New Zealand (4,466,424)
Population Density
1. United Kingdom (257.13 people per square kilometres)
2. U.S.A. (31.95 people per square kilometres)
3. New Zealand (16.62 people per square kilometres)
4. Canada (3.45 people per square kilometres)
5. Australia (2.99 people per square kilometres)
I was asked to supply a chart (graph). This column graph has been inserted to show relative population densities, including Japan mentioned in the comment section.
.
Can you see the smallest country by area has the highest population density? (N.B. Adding Japan changed this slightly as it became the third smallest country by area yet had the highest population density.)
We must remember, when looking at Canada and Australia and their low population densities, Canada has large parts of the country in Arctic regions and Australia has large areas of desert. Below is a link I made comparing Great Britain and Australia. It gives information about Australia and its land.
https://rossmannellcomments.edublogs.org/2013/05/06/great-britain-and-australia-compared-for-our-world-our-numbers/
A World Without Numbers
This was a very early blog comment post on another blog. It has been transferred to this blog.
Schools and students have permission to use this graphic for non-commercial, educational purposes.
In answer to the question, "If you woke up tomorrow and there was no such thing as numbers, what would your day be like?"
There were, in the past, times when numbers weren't in existence. They're something humans have made up to try to explain things we see.
Through history, there have been many ways of writing numbers. Our numbers are known as Hindu-Arabic because of the influence of those two systems on us. They replaced Roman numerals that were based on fives as in the fingers and thumbs on our hands.
Look at the sum below and see how hard it would be to do maths....
Roman Numerals
DCCLXIX + CCCXLIV = MCXIII
Hindu-Arabic Numerals
769 + 344 = 1113
Which would you prefer to use?
Did you know computers use a number system called binary to work?
Binary only uses 1 and 0. A 1 tells the computer to turn something on and a 0 off. By turning on or off many tiny “switches” in a processor, the computer is able to operate. No numbers, no computers.
Here is 0 to 10 in binary coding…
0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010
Numbers are a fascinating part of our lives. They are much more a part of our everyday life than we might realise and would affect many things you might not realise.
Remember to set your alarm so you can be up in time for school tomorrow. Wait, clocks use numbers. Have a shower, no, computers and machines control the delivery of water and electricity. Maybe we could walk to school because buses and cars aren’t running. Wait, the buildings have gone because we didn’t have the numbers to help build them. We can go into the simple wooden shelter and sit on the ground then pick up our books. No, computers and machines involved again…
Maybe I should just make a spear and settle around a fire near my rough shelter made from branches and animal skins. When the sun rises, I’ll go hunting while the family searches for water and wild grains to make rough bread. For games, my children can practise throwing spears or learn how to cut animal skins into clothing.
We could survive without numbers but the world would be a very different place for us.
Older Australian Currency for “Our World, Our Numbers”
"Our World, Our Numbers" is a mathematics collaboration project involving 7 classes in 5 countries. The first post was from 4KM and 4KJ in Australia
Australian Currency
Dear 4KM and 4KJ,
A second of your posts for 2013 started me thinking in different directions again. Did you know when I was your age I used different Australian money to what we have today?
When I was your age, we used pounds, shillings and pence, not dollars and cents. I have some pictures of the money down below. There was also a £10 (10 pound) note but I don’t have one in my collection. While we aren’t allowed to copy our modern money, I think these are okay because the last time they were used was in 1966.
You can click on the pictures to enlarge them.
From left to right...
TOP ROW
half penny (ha'penny) equal to about half a cent
penny equal to about 1 cent
Three penny - 3d (thrupence) equal to about 2.5 cents
BOTTOM ROW
Sixpence equal to 5 cents
One shilling - 1s equal to 12 pennies and became 10 cents
Florin - two shillings equal to 24 pennies and became 20c
10 shillings - half a pound - 120 pennies - became $1
One Pound - £1 - 20 shillings - 240 pennies - became $2
Five Pound - £5 - 100 shillings - 1200 pennies - became $10
There was a 10 pound (£10) note but I don't have one in my collection. It became $20.
When these pounds (£), shillings (s) and pence (d) were in use and I was your age, my father earned about £20 (20 pounds) a week. That was enough to make payments on the house and car, buy clothes and groceries, save some and go on holidays. That is $40 in today's currency. My pocket money was 1s (one shilling or ten cents) a week. Prices were much lower than today but we earned much less. The money shown above would have been about one third of my father's weekly pay yet it was only £6/13/10 ($13.38). Click below to hear how the money was said...
Money
On the 14th February, 1966, Australia started using decimal currency. We had 6 types of coins and 5 notes. At that time, all notes were paper and not the plastic we use today.
Coins: 1c, 2c, 5c, 10c, 20c, 50c
Notes: $1, $2, $5, $10, $20
Here are pictures of the 1c and 2c coins plus $1 and $2 note no longer used. Australian coins have the face of the ruling monarch on the opposite sides, i.e. Queen Elizabeth II since her coronation in 1952.
1 cent and 2 cent coins
$1 note
$2 note
Australian Decimal Money Timeline
1966 - Decimal currency introduced on February 14
1973 - $50 note introduced
1984 - $1 coin replaces the note
1988 - Australia's first polymer (plastic) notes appeared
1988 - $2 coin replaces the note
1992 - 1c and 2c no longer officially in use
1996 - $100 note introduced
Money Links
Royal Australian Mint
Museum of Australian Currency Notes
* Schools and students have permission to use the graphics on this post for non-commercial, educational purposes.
None of the notes shown are now legal tender.
“Wrong” shapes for 4KM and 4KJ
To see the 4KM and 4KJ post...
Learning About Shape
Hello 4KM and 4KJ,
I found your post on shapes interesting. Many times my classes had looked at the properties of 2D and 3D shapes. I have also had to draw shapes very many times but some of my favourites include 3D shapes we might be able to draw on paper but they don't make sense in the real world. Here are two examples.
If I were to cut out a triangle and a hexagon from a piece of timber, paint the triangle red and the hexagon blue then place one on top of the other, would they appear as below? What is wrong with this picture?
Schools and students have permission to use this graphic for non-commercial, educational purposes.
Some 3D shapes we draw can be impossible in the real 3D world. Below is a shape known as a blivet. Look at it carefully. What did you notice?
Schools and students have permission to use this graphic for non-commercial, educational purposes.
Is it important to use time wisely? – A philosophical question posed for Miriam Lord Community School students
To view the original Miriam Lord Community School blog post...
Is it important to use time wisely?
N.B. I have never studied philosophy and am not an expert in the field of thought. Below are just some ideas from my wandering mind.
Hello Miriam Lord Community School,
What an interesting philosophical question, “Is it important to use time wisely?”
Before looking at the overall question, let’s look at the parts within…
Important – meaning: of significance or consequence – Judgement of importance can depend on who is judging the importance. If we use our "feelings" to judge we are making a subjective judgement, i.e. a judgement made by one person often influenced by emotion.
Time – Time is a creation of humanity dating well back in our history. I won’t unwisely use time here. I recently created a post about time for another class. Here’s the link…
Learning About Time
Wisely – wise: having the power of discerning and judging as to what is true or right. – Wisdom is something we can develop through learning and experience although there are those in our world who seem to grow into adults without the ability to make wise choices. As in "important", there can be subjectivity here although, more importantly, wisdom mostly includes objective judgement. Objective judgements are made when we way up the information or need in order to decide the best choice. It isn’t an emotional a choice like a subjective one.
(Word definitions are taken from "The Concise Macquarie Dictionary")
Now for the overall question…
“Is it important to use time wisely?”
Yes.
Seems a simple answer yet, we must remember, we make choices based on our subjective and objective judgements. When we are young, we don't have the experiences to make objective judgements a strong part of our choices so we rely more on subjective judgements.
…but this game is important.
I like this TV programme.
…but my friends want to play.
As we grow, we experience more of life. We start to see the “bigger picture”. Our judgements start to become more objective.
I love this game but the assignment is due soon and must be done. The game can wait.
I like this TV programme but there is a documentary on at the same time that will help me with one of my subjects.
My friends want to play but I know I should be helping my parents pack for our move.
If a teacher were to say you weren’t using your time wisely, they mean they see the bigger picture and see the importance of other tasks in achieving goals. You might see the smaller picture but, in time, you will grow in experience and understand the advice given by others.
Is it wasting time to spend 10 minutes lying on your back and looking up at the sky?
No, this time out is like meditation. It can allow us to organise our thoughts or help us to relax for a task ahead.
Yes, if we have an appointment in five minutes then we are wasting time.
Is watching TV wasted time?
No, this can be a time of relaxation after a hard day of tasks or you might be watching an important programme relating to your work.
Yes, when you know you must be preparing a project due the next day.
Is playing with friends a waste of time?
No, playing with friends helps us build links with those who will support us when in need. Being with friends is important in our social growth. Humans are social creatures.
Yes, if we know we should have been home earlier and our parents might be worried.
Philosophical questions are not so much a matter of getting the “correct” answer. The questions are designed to make us think.
From your school blog "Remember: Good philosophers PEE – make their POINT, EXPLAIN and give an EXAMPLE."
Here’s another philosophical question relating to your question….
“Can two people come up with different answers yet both be correct?”
My answer again, yes or no. Can you think why?
Schools and students have permission to use this graphic for non-commercial, educational purposes.
Why 24 hours in a day? Why not 10 or 100? – for 4T learning about time
For 4T's original post...
http://mrstoddsclass.blogspot.com.au/2012/09/learning-about-time.html?spref=tw
Hello 4T,
Time is an interesting topic. It seems so simple at first but why are there 24 hours in a day? Why not 200 hours or 10 hours? Why are there 60 minutes in an hour? Why not 100 minutes?
Schools and students have permission to use this graphic for non-commercial, educational purposes.
The time is 48 minutes past 7. That is 07:48.
What do I know about time?
I had often wondered why we had 24 hours in a day. From what I have been able to find out, one explanation comes from the Ancient Egyptians giving us the 24 hour day.
We count in what is called base 10 using the digits 0 to 9 (10 digits). The Ancient Egyptians counted in base 12. They divided the day into 12 hours of day and 12 hours of night.
Here is a link about the 24 hour day…
http://curious.astro.cornell.edu/question.php?number=594
Another suggestion is the times came from the Ancient Babylonians. Unlike the Egyptians, they counted in base 60. 6, 12, 60 and 360 were important for them. They had 12 signs of the zodiac in the sky, divided the day into 12 hours of day and 12 hours of night, had 60 minutes in an hour and divided circles into 360 parts. Here is a link to the answer…
http://answers.yahoo.com/question/index?qid=20070323094436AAQMp8M
I think I prefer the Babylonian explanation better as it covers extra important numbers. Even though we now use base 10 numbers, we have kept the old divisions of the day for thousands of years.
With all of the above, where do we get a.m. and p.m.?
a.m. comes from the Latin “ante meridiem” meaning before midday
p.m. comes from the Latin “post meridiem” meaning after midday
In my diary, I like to use 24 hour time. 2:30 can be in the morning or afternoon unless we add a.m. or p.m.. 24 hour time makes it easier for me…
02:30 or 0230 – is 2:30 a.m.
14:30 or 1430 – is 2:30 p.m.
When is the best time of the day?
For me, the best time of day isn’t any set time. It’s when I’m doing something I enjoy whether commenting on blogs, writing stories, hiking in a national park, going to the cinema, listening to music as I work, making DVDs or speaking to friends.
What is my favourite time?
00:00 (that’s midnight) because I have usually logged off the computer for the night or 06:00 when I normally wake in the morning to see what has been happening in the world.
Keep blogging, everyone. I enjoyed your time post.
@RossMannell
Teacher (retired), N.S.W., Australia
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
I just had another thought to add to this post... If we did have 10 hours in a day, 5 for the day and 5 for the night, 100 minutes in an hour and 100 seconds in a minute what difference would we see in the amount of minutes and seconds in a day?
24 hours, 60 minutes, 60 seconds
24 hours = 24 x 60 minutes = 1,440 minutes = 1,440 x 60 seconds = 86,400 seconds in a day
1 day has 24 hours or 1,440 minutes or 86,400 seconds
10 hours, 100 minutes, 100 seconds
10 hours = 10 x 100 minutes = 1,000 minutes = 1,000 x 100 seconds = 100,000 seconds in a day
1 day has 10 hours or 1000 minutes or 100,000 seconds
This means there would be 440 less minutes in the 10 hour day but 13,600 seconds more. It's easier to work out the numbers for a 10 hour day. Our modern time might have been very different if the Babylonians and Egyptians had base 10 numbers like us.
Which do you think is better, the 24 hour or 10 hour day?
Symmetry (almost) in Nature – for the Mindful Monkeys
For the original post...
http://maraekakahoschool2.blogspot.co.nz/2012/07/super-symmetry.html
Hello Mindful Monkeys,
I enjoyed viewing the slideshow of your adventures into symmetry. In your post, you asked if I was symmetrical. That started me thinking if I could find some living things with symmetry. I came very close with three photos from my photo collection. The images blow are of a wallaby, butterfly and flower taken when I have been hiking around my town. Each set of images show the original at the top. I then took each half of the main image, duplicated each half then flipped one of each. On the left of each set you will see what two left sides look like when joined together. On the right is an image made of two right sides.
I think these three living things are very close to symmetrical. What do you think?
You can click on an image to see it a little larger.
Schools and students have permission to use this graphic for non-commercial, educational purposes.
Schools and students have permission to use this graphic for non-commercial, educational purposes.
Schools and students have permission to use this graphic for non-commercial, educational purposes.